Coding GraphSAGE From Scratch
In the previous blog post, we took a short, intuitive look at the basics of Graph Neural Networks (GNNs), and at the end got a look at some pseudocode for a popular classical GNN architecture, GraphSAGE. In this post, we will go through a from-scratch Python implementation of the entire GraphSAGE algorithm, building up each step of message passing and connecting real lines of Pytorch code to lines of the original pseudocode algorithm.

As a quick note: since we are writing our code from scratch for understanding, it will end up being a bit more verbose than necessary. In practice, many operations are abstracted away, hidden under-the-hood by GNN libraries like Pytorch Geometric (PyG) [1], allowing us to just focus on the details of our GNN and data which we care about. Our code will not use any data structures or layers from PyG for simplicity, so that only an understanding of Pytorch and Python class-based definitions is necessary to read the code snippets.
The goal by the end of this coding tutorial is to feel comfortable looking at code implementations of PyG-style message-passing. Afterwards, the jump to looking at real source code of different GNNs in PyG (docs) will feel easier, which will enable you to read more GNN papers and make more connections to real code! If you end up using an alternative GNN library other than PyG in your research (or an alternative library to Pytorch, or another programming language altogether!), don’t worry, the general idea of message-passing operations should carry over sufficiently well to other implementations.
Starting out: Input graph information
To start out, let’s revisit the molecular graph example which we saw in the previous post:
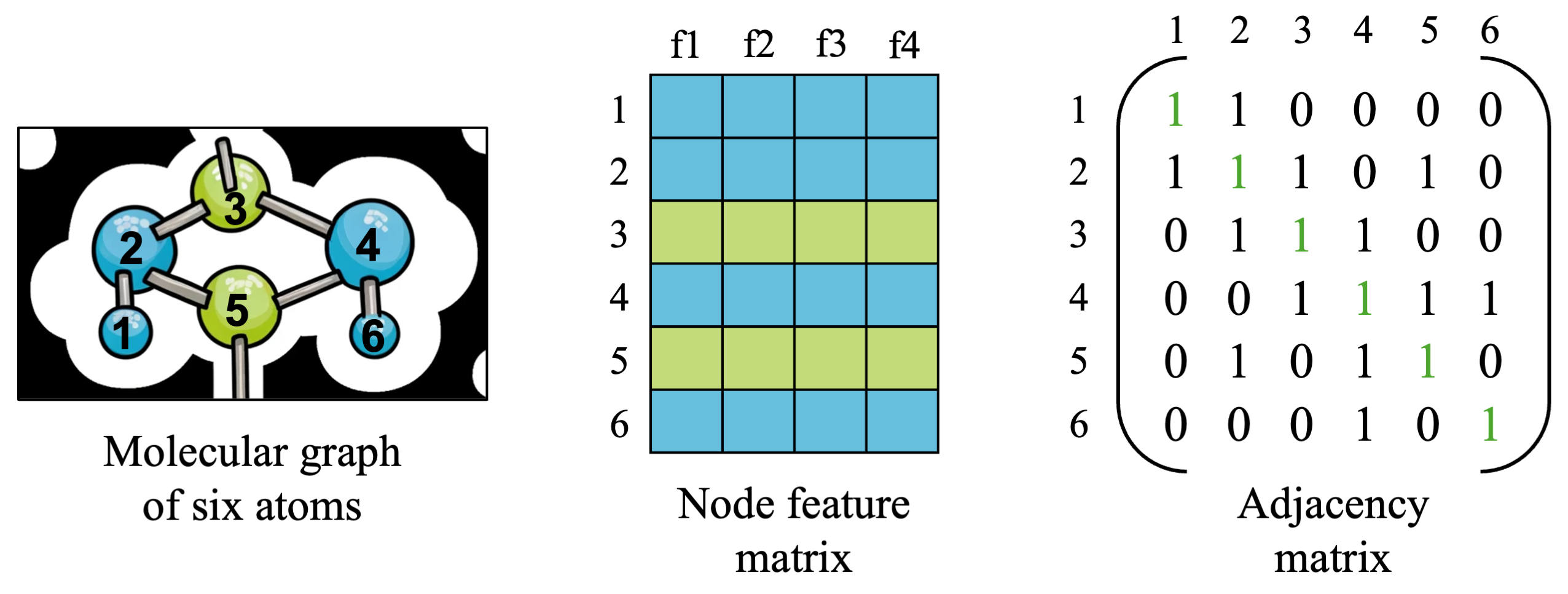
We will build our graph input example from this example, for familiarity. The graph will consist of 6 nodes representing hydrogen (blue) and carbon (C) atoms, each with four features: atomic number, atomic mass, (made-up) charge values, and number of incoming edges. We also have the same adjacency matrix from before, with 18 edges in total connecting nodes together, including self-edges.
We can initialize our node feature matrix and adjacency matrix as Pytorch tensors in our Python code as follows:
# Define input node feature matrix and adjacency matrix
input_node_feature_matrix = torch.tensor([
[1.0, 1.0078, 1, 2], # atomic number, atomic mass, charge, and number of bonds
[1.0, 1.0078, 1, 4],
[6.0, 12.011, -1, 3],
[1.0, 1.0078, 0, 4],
[6.0, 12.011, -1, 3],
[1.0, 1.0078, 1, 2],
], dtype=torch.float32) # [num_nodes, num_features]
binary_adjacency_matrix = torch.tensor([
[1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0],
[0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 1],
[0, 1, 0, 1, 1, 0],
[0, 0, 0, 1, 0, 1],
], dtype=torch.int64) # [num_nodes, num_nodes]
These two Pytorch tensors contain all of the information we need about node features as well as graph connectivity. You’ll notice, however, that the adjacency matrix contains many zero values, which gets worse as we scale to much larger graphs (millions and billions of nodes!) since nodes tend to be connected to only a few other nodes.
Because of this, we often opt for an edge list representation of graph connectivity information, where instead of a [num_nodes, num_nodes] matrix containing many zeros for missing edges, we transform it into an edge list of shape [2, num_edges], which specifies the index of the start (source) and end (destination) node for each existing edges. With this representation, we only store two pieces of information for edges that actually exist, rather than 1 piece of information for every possible edge that might exist in the graph. Libraries such as PyG opt for this edge list representation, which they call an edge_index, so we will define a conversion function ourselves to turn an adjacency matrix into an edge_index tensor as follows:
def adj_matrix_to_sparse_edge_index(adj_matr: torch.Tensor):
"""
This function takes a square binary adjacency matrix, and returns an edge list representation
containing source and destination node indices for each edge.
Arguments:
adj_matr: torch Tensor of adjacency information, shape [num_nodes, num_nodes], dtype torch.int64
Returns:
edge_index: torch Tensor of shape [2, num_edges], dtype torch.int64
"""
src_list = []
dst_list = []
for row_idx in range(adj_matr.shape[0]):
for col_idx in range(adj_matr.shape[1]):
if adj_matr[row_idx, col_idx].item() > 0.0:
src_list.append(row_idx)
dst_list.append(col_idx)
return torch.tensor([src_list, dst_list], dtype=torch.int64) # [2, num_edges]
edge_index = adj_matrix_to_sparse_edge_index(binary_adjacency_matrix) # [2, num_edges]
Defining our message-passing layer
Now that we have our input node feature and edge_index tensors, we can move on to defining our message-passing layer which will implement the GraphSAGE message-passing algorithm. If we look at the pseudocode at the beginning, we can see that in the main message-passing logic happens in two lines of pseudocode, which happen for each node in the graph:
- \[h_{N(v)}^{k+1} = AGGREGATE({h_u^k, \forall u \in N(v)})\]
- \[h_v^{k+1} = \sigma(W \cdot CONCAT(h_v^k, h_{N(v)}^{k+1}))\]
These two lines of code define mathematically how we will do message passing, specifying the steps of message-passing which we previously covered: assuming (1) messages have been created, we (2) aggregate messages from neighboring nodes to get \(h_{N(v)}^{k+1}\), and (3) update representations, ending up with \(h_v^{k+1}\).
To implement this in code, we will need an organized definition of the message, aggregate, and update steps. In Pytorch-style coding, neural network layers are typically defined in Python class syntax, where we define a Python class which will house our GNN layer:
class GraphSAGELayer(nn.Module):
def __init__(self, in_dim: int, out_dim: int):
super().__init__()
# Define linear layers parameterizing neighbors and self-loops
self.lin_neighbors = nn.Linear(in_dim, out_dim, bias=True)
self.lin_self = nn.Linear(in_dim, out_dim, bias=True)
Here we have defined a Python class called GraphSAGELayer, which inherits from Pytorch’s torch.nn.Module class. This Module class lets us inherit functionalities for neural network that will allow us to train our model using stochastic gradient descent, along with all of Pytorch’s other functionalities.
Looking again at the two pseudocode lines, we can see that the only learnable parameters in GraphSAGE is a weight matrix \(W\), which parameterizes a concatenation of a node’s own embedding \(h_v^k\) with its neighborhood embedding \(h_{N(v)}^{k+1}\). In practice, GraphSAGE is implemented in Pytorch Geometric (here) using two linear layers for neighboring message embeddings and a node’s self embedding. The reason for this might be twofold: (i) having two separate layers leaves an option to not have a self-embedding weight, which can be desirable sometimes, and (ii) sometimes we may want separate weights parameterizing self-connections, which can be seen as a form of skip-connections for GNN embeddings.
In our code, we will call these two linear layers lin_neighbors and lin_self, as shown above. Now comes an important part: how do we implement logic to create and pass messages, and aggregate embeddings for neighbors in order to obtain \(h_{N(v)}^{k+1}\)? We can define our own function for message-passing as follows:
def message_passing(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
This function is responsible for passing messages between nodes according to the edges
in 'edge_index'.
- Messages from the source --> destination node consist of the source nodes feature vector.
- Sum aggregation is used to aggregate incoming messages from neighbors.
Arguments:
x: torch Tensor of node representations, shape [num_nodes, hidden_size], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
Returns:
neigh_embeds: torch Tensor of aggregated neighbor embeddings, shape [num_nodes, hidden_size], dtype torch.float32
"""
src_node_indices = edge_index[0, :] # shape [num_edges]
dst_node_indices = edge_index[1, :] # shape [num_edges]
# Step (1): Message
src_node_feats = x[src_node_indices] # shape [num_edges, hidden_size]
# Mean aggregation
neighbor_sum_aggregations = []
for dst_node_idx in range(x.shape[0]): # loop over destination nodes
# find incoming edges, get incoming messages from source nodes
incoming_edge_indices = torch.where(dst_node_indices == dst_node_idx)[0] # find incoming edges
incoming_messages = src_node_feats[incoming_edge_indices] # shape [num_incoming_edges, hidden_size]
# Step (2): Aggregate - sum messages from neighbors (if > 1 neighbors)
incoming_messages_summed = incoming_messages.sum(dim=0) if incoming_messages.shape[0] > 1 else incoming_messages
neighbor_sum_aggregations.append(incoming_messages_summed)
neigh_embeds = torch.stack(neighbor_sum_aggregations) # [num_nodes, hidden_size]
return neigh_embeds
This function is quite involved, so we will go through step-by-step, and point out where code connects to pseudocode with comments. We can see that the inputs to this function are our node feature matrix x, and the edge_index, which we already have from earlier. The function definition states that we will take these two tensors as input, and we will eventually return \(h_{N(v)}^{k+1}\).
The first thing we need to do is organize how our nodes are going to pass messages to each other, for Step (1): Message. The simplest message which one node can pass to another node is its node embedding (which is also the case in GraphSAGE), so we first get the indices of our source nodes from our edge_index, and use that to index into our node feature matrix x. If you are familiar with array indexing in Pytorch, you’ll realize that this gives us a [num_edges, hidden_size] tensor, effectively giving us a tensor containing source node embeddings. This is an important step, because with the leading dimension being num_edges rather than num_nodes, we can do edge operations and deal with passing messages along edges.
With this indexing operation, our first step of message creation is already complete, since we are using source node embeddings as the message to be passed. Now, we need to perform the next step, which is to aggregate embeddings for each destination node using a permutation-invariant aggregator. We will use sum aggregation here, since it is a more expressive aggregation function (more on that another time!), which means for each destination node in the graph, we need to sum all incoming message embeddings. We accomplish this by looping over destination nodes, finding which edges are ending at that destination node, and summing the corresponding messages. The resulting variable, neigh_embeds, directly corresponds to \(h_{N(v)}^{k+1}\) in the pseudocode.
We can complete our message-passing layer implementation by writing a forward() function, which tells Pytorch how we want a forward pass through our neural network to be implemented:
def forward(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
Implementation for one message-passing iteration for GraphSAGE.
Arguments:
x: torch Tensor of node representations, shape [num_nodes, hidden_size], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
Returns:
out: torch Tensor of updated node representations, shape [num_nodes, hidden_size], dtype torch.float32
"""
x_message_passing, x_self = x, x # duplicate variables pointing to node features
neigh_embeds = self.message_passing(x_message_passing, edge_index)
neigh_embeds = self.lin_neighbors(neigh_embeds)
x_self = self.lin_self(x_self)
# # Step (3): Update - sum concatenation to update node representations
out = neigh_embeds + x_self
return out
With the message_passing() function doing the heavy lifting, all we need to do in the forward() function is call the function message passing, and then perform step 3, which is updating node representations. This is done by running \(h_{N(v)}^{k+1}\) and \(h_v^k\) through their respective linear layers, and then concatenating them together. In practice, concatenation operations are done either through summing vectors together, or by joining two vectors together (resulting in a longer vector). I have not seen a preference for either method for concatenation in code implementations thus far.
Completing a 1-layer GraphSAGE model
Now that we have defined a full message-passing class using simple operations, we can complete a full 1-layer GNN model by defining a second class which will use our just-completed message passing layer definition:
class GraphSAGEModel(nn.Module):
def __init__(self, in_features: int, hidden_size: int, out_features: int, dropout: int = 0.1):
super().__init__()
self.input_proj = nn.Linear(in_features, hidden_size, bias=True)
self.conv1 = GraphSAGELayer(in_dim=hidden_size, out_dim=hidden_size)
self.act1 = nn.ReLU()
self.drop1 = nn.Dropout(p=dropout)
self.lin_out = nn.Linear(hidden_size, out_features, bias=True)
def forward(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
Forward pass implementation of 1-layer GraphSAGE model.
Arguments:
x: torch Tensor of input node features, shape [num_nodes, num_features], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
"""
x = self.input_proj(x) # Input projection: [num_nodes, num_features] --> [num_nodes, hidden_size]
x = self.conv1(x, edge_index) # Message-passing
x = self.act1(x)
x = self.drop1(x)
x = self.lin_out(x)
return F.log_softmax(x, dim=-1) # softmax over last dim for classification
This class again inherits from nn.Module, and it defines 1 layer of message-passing by calling the GraphSAGELayer() class we just defined above. It also defines several other components, such as a ReLU nonlinearity after the message-passing layer, a dropout layer, and input/output projections. This definition is for a classification model with 1-message passing layer; if we wanted to change the task the model is built for, we could change the output head and remove the final softmax layer as we need depending on our task. If we have a need to pass messages multiple times, we can simply define more layers of our GraphSAGELayer class to pass messages more times! Note that this would mean not sharing weights for different message-passing iterations, which is common practice.
Putting everything together
We can now put everything together by defining an instance of our 1-layer GraphSAGE model and doing a full forward pass on our example graph! The full code is below, and is also available on GitHub:
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.data import Data
class GraphSAGELayer(nn.Module):
def __init__(self, in_dim: int, out_dim: int):
super().__init__()
# Define linear layers parameterizing neighbors and self-loops
self.lin_neighbors = nn.Linear(in_dim, out_dim, bias=True)
self.lin_self = nn.Linear(in_dim, out_dim, bias=True)
def message_passing(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
This function is responsible for passing messages between nodes according to the edges
in 'edge_index'.
- Messages from the source --> destination node consist of the source nodes feature vector.
- Sum aggregation is used to aggregate incoming messages from neighbors.
Arguments:
x: torch Tensor of node representations, shape [num_nodes, hidden_size], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
Returns:
neigh_embeds: torch Tensor of aggregated neighbor embeddings, shape [num_nodes, hidden_size], dtype torch.float32
"""
src_node_indices = edge_index[0, :] # shape [num_edges]
dst_node_indices = edge_index[1, :] # shape [num_edges]
# Step (1): Message
src_node_feats = x[src_node_indices] # shape [num_edges, hidden_size]
# Mean aggregation
neighbor_sum_aggregations = []
for dst_node_idx in range(x.shape[0]): # loop over destination nodes
# find incoming edges, get incoming messages from source nodes
incoming_edge_indices = torch.where(dst_node_indices == dst_node_idx)[0] # find incoming edges
incoming_messages = src_node_feats[incoming_edge_indices] # shape [num_incoming_edges, hidden_size]
# Step (2): Aggregate - sum messages from neighbors (if > 1 neighbors)
incoming_messages_summed = incoming_messages.sum(dim=0) if incoming_messages.shape[0] > 1 else incoming_messages
neighbor_sum_aggregations.append(incoming_messages_summed)
neigh_embeds = torch.stack(neighbor_sum_aggregations) # [num_nodes, hidden_size]
return neigh_embeds
def forward(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
Implementation for one message-passing iteration for GraphSAGE.
Arguments:
x: torch Tensor of node representations, shape [num_nodes, hidden_size], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
Returns:
out: torch Tensor of updated node representations, shape [num_nodes, hidden_size], dtype torch.float32
"""
x_message_passing, x_self = x, x # duplicate variables pointing to node features
neigh_embeds = self.message_passing(x_message_passing, edge_index)
neigh_embeds = self.lin_neighbors(neigh_embeds)
x_self = self.lin_self(x_self)
# # Step (3): Update - sum concatenation to update node representations
out = neigh_embeds + x_self
return out
class GraphSAGEModel(nn.Module):
def __init__(self, in_features: int, hidden_size: int, out_features: int, dropout: int = 0.1):
super().__init__()
self.input_proj = nn.Linear(in_features, hidden_size, bias=True)
self.conv1 = GraphSAGELayer(in_dim=hidden_size, out_dim=hidden_size)
self.act1 = nn.ReLU()
self.drop1 = nn.Dropout(p=dropout)
self.lin_out = nn.Linear(hidden_size, out_features, bias=True)
def forward(self, x: torch.Tensor, edge_index: torch.Tensor):
"""
Forward pass implementation of 1-layer GraphSAGE model.
Arguments:
x: torch Tensor of input node features, shape [num_nodes, num_features], dtype torch.float32
edge_index: torch Tensor of graph connectivity information, shape [2, num_edges], dtype torch.int64
"""
x = self.input_proj(x) # Input projection: [num_nodes, num_features] --> [num_nodes, hidden_size]
x = self.conv1(x, edge_index) # Message-passing
x = self.act1(x)
x = self.drop1(x)
x = self.lin_out(x)
return F.log_softmax(x, dim=-1) # softmax over last dim for classification
def adj_matrix_to_sparse_edge_index(adj_matr: torch.Tensor):
"""
This function takes a square binary adjacency matrix, and returns an edge list representation
containing source and destination node indices for each edge.
Arguments:
adj_matr: torch Tensor of adjacency information, shape [num_nodes, num_nodes], dtype torch.int64
Returns:
edge_index: torch Tensor of shape [2, num_edges], dtype torch.int64
"""
src_list = []
dst_list = []
for row_idx in range(adj_matr.shape[0]):
for col_idx in range(adj_matr.shape[1]):
if adj_matr[row_idx, col_idx].item() > 0.0:
src_list.append(row_idx)
dst_list.append(col_idx)
return torch.tensor([src_list, dst_list], dtype=torch.int64) # [2, num_edges]
if __name__ == "__main__":
# Define input node feature matrix and adjacency matrix
input_node_feature_matrix = torch.tensor([
[1.0, 1.0078, 1, 2], # atomic number, atomic mass, charge, and number of bonds
[1.0, 1.0078, 1, 4],
[6.0, 12.011, -1, 3],
[1.0, 1.0078, 0, 4],
[6.0, 12.011, -1, 3],
[1.0, 1.0078, 1, 2],
], dtype=torch.float32)
binary_adjacency_matrix = torch.tensor([
[1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0],
[0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 1],
[0, 1, 0, 1, 1, 0],
[0, 0, 0, 1, 0, 1],
], dtype=torch.int64)
edge_index = adj_matrix_to_sparse_edge_index(binary_adjacency_matrix)
print("input_node_feature_matrix:", input_node_feature_matrix.shape)
print(input_node_feature_matrix)
print("binary_adjacency_matrix:", binary_adjacency_matrix.shape)
print(binary_adjacency_matrix)
print("edge_index:", edge_index.shape)
print(edge_index, "\n")
# Define GraphSAGE model
model = GraphSAGEModel(
in_features=4, # 4 input features per node
hidden_size=16, # 16-dimensional latent vectors
out_features=2 # 2 classes of nodes in our example: Carbon and Hydrogen
)
print("\nModel:")
print(model, "\n")
# Forward pass & loss calculation for node classification
output = model(x=input_node_feature_matrix, edge_index=edge_index)
atom_labels = torch.tensor([0, 0, 1, 0, 1, 0], dtype=torch.int64) # 0 = Hydrogen, 1 = Carbon
loss = F.nll_loss(output, target=atom_labels)
print("Loss value: {:.5f}".format(loss.item()))
Wrapping up
I hope this code tutorial was useful for you! Many of these operations are abstracted away under the hood of GNN libraries, however understanding the underlying operations going on during message-passing the first step to being able to adapt and improve the algorithm as per your needs and goals. If the code snippets make sense, and you succeed in running them and looking at the printed outputs, I would highly enourage you to look at real source code for GNNs in Pytorch Geometric, for instance the GraphSAGE implementation. You will notice that PyG exposes certain functions, such as message(), allowing developers to override these functions to inject custom behavior during message-passing. It is a clever software engineering design that allows developers to build custom GNN models which still abstracting low-level operations away from us, like aggregating neighboring nodes based on edges.
As always, feedback is welcome and appreciated on this code tutorial at: syed [dot] rizvi [at] yale [dot] edu
References
- Fey, Matthias, and Jan Eric Lenssen. “Fast graph representation learning with PyTorch Geometric.” arXiv preprint arXiv:1903.02428 (2019).